The Geometry of catapults

Join me in this week’s STEM video, the Geometry of Catapults, as I take you on a math adventure to discover amazing insights into how our catapults work, and what we can do to tune the distance or range that our projectiles reach.

By looking at the transfer of Potential Energy into Kinetic Energy, we discover that our projectile velocity will increase as the spring constant of our rubber band increases, as the mass of our projectile decreases, and as the elongation of our rubber band increases.

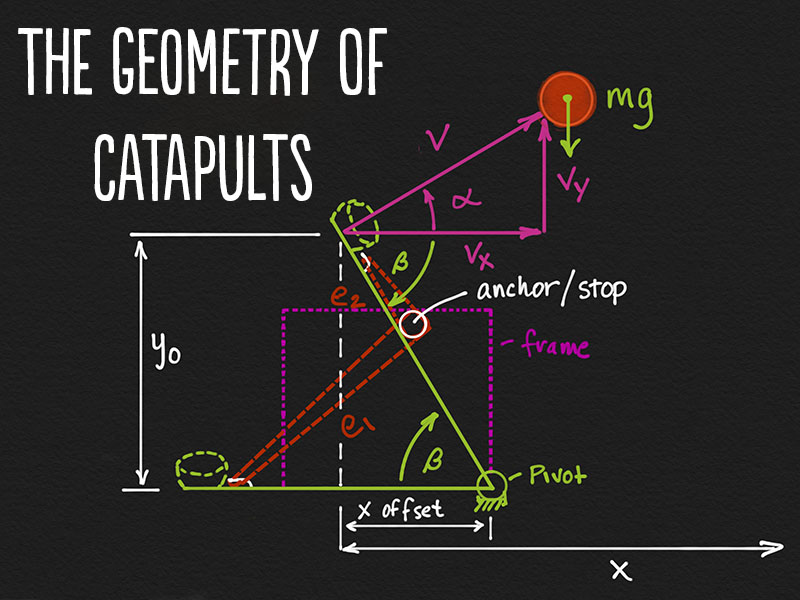
Next we look at the effect of launch angle on our projectile’s trajectory and total distance traveled. We learn that the launch angle, alpha, controls how much velocity goes into a horizontal component of velocity versus a vertical component of velocity.

We learn that both have an affect on distance traveled, because the horizontal distance traveled, x, is equal to the horizontal component of velocity times the time to fall… which is related to the vertical component of velocity.

We can solve for the time to fall using the quadratic equation in y as a function of the vertical component of velocity and the initial height, y0, of the projectile. We can increase the time to fall by increasing the vertical component of velocity or the initial height, y0, of our projectile at launch. Here’s my crib sheet of key equations:

But if our question is how to maximize X (the horizontal distance traveled), what’s the optimum launch angle? 

Good question! That’s for you to test. I take you through a few examples, using the velocity I measured from one of my catapult tests using video shot against a gridded background.  

For a given initial vertical offset, y0, and total velocity, v=129 inches per second, here’s what the effect of different launch angles looks like:

So, by studying the physics and the geometry of our catapult, we’ve gained insights into what we can do to adjust the range of our projectiles. If we need more distance (range), we can:

• decrease the mass (weight) of our projectile, m
• increase the spring constant of our rubber band (thicker rubber band, or add a second)
• increase the elongation (stretch) of our rubber band
• increase the initial vertical offset, y0, to increase the time to fall
• look at the effect of changing launch angle, as this will shift the balance of horizontal velocity (drives horizontal distance) and vertical velocity (which will increase hang time).

In the next video, we’ll take a look at the effect of variation in our data and see how different test conditions create larger or smaller amounts of scatter.

FYI – I was just featured on the STEM Everyday Podcast with Chris Woods. Here’s the link:

Cheers!

Marsha Tufft